آنالیز آماری

آزمون آنوا (ANOVA) چیست و چرا اهمیت دارد؟

در دنیای تحلیل داده‌ها، زمانی که می‌خواهیم میانگین‌های سه گروه یا بیشتر را با یکدیگر مقایسه کنیم، آزمون آماری تحلیل واریانس یا به اختصار آنوا (ANOVA) به کمک ما می‌آید. این آزمون قدرتمند، ابزاری کلیدی در آمار استنباطی محسوب می‌شود و به محققان در زمینه‌های مختلف کمک می‌کند تا تفاوت‌های معنادار بین گروه‌ها را تشخیص دهند.

اگر تا به حال با این سوالات روبرو شده‌اید:

• آیا روش‌های مختلف تدریس بر عملکرد دانش‌آموزان تاثیر متفاوتی دارند؟
• آیا سه نوع مختلف کود شیمیایی بر میزان محصول کشاورزی اثرات یکسانی دارند؟
• آیا میانگین رضایت مشتریان از سه نوع مختلف خدمات ارائه شده تفاوت معناداری دارد؟
• آیا سه روش تمرین بر سطوح قند خون ناشتا زنان مبتلا به دیابت نوع دو اثرات یکسانی دارد؟

پاسخ این سوالات و بسیاری موارد مشابه، با استفاده از آزمون آنوا قابل بررسی است.

اصول اساسی آزمون آنوا

ایده اصلی در پس آزمون آنوا، مقایسه واریانس (پراکنش) داده‌ها بین گروه‌ها با واریانس درون هر گروه است. به عبارت ساده‌تر، این آزمون بررسی می‌کند که آیا تفاوت‌های مشاهده شده بین میانگین گروه‌ها به دلیل یک اثر واقعی است یا صرفاً ناشی از تغییرات تصادفی در نمونه‌ها.

فرضیات کلیدی آزمون آنوا:

برای اینکه نتایج آزمون آنوا معتبر باشد، باید چند فرضیه اساسی برقرار باشند:

1. استقلال مشاهدات: داده‌های هر گروه باید مستقل از داده‌های گروه‌های دیگر باشند.
2. نرمال بودن توزیع: داده‌های هر گروه باید تقریباً دارای توزیع نرمال باشند. (در نمونه‌های بزرگ، این فرض تا حدودی قابل چشم‌پوشی است – قضیه حد مرکزی).
3. برابری واریانس‌ها: واریانس (پراکندگی) داده‌ها در تمام گروه‌ها باید تقریباً برابر باشد (همگنی واریانس‌ها).

مراحل اجرای آزمون آنوا

اجرای آزمون آنوا معمولاً شامل مراحل زیر است:

1. تعریف فرضیه‌های آماری:
   • فرضیه صفر (H₀): میانگین تمام گروه‌ها با یکدیگر برابر است. (μ1​=μ2​=μ3​=…=μk​)
   • فرضیه یک (H₁): حداقل میانگین دو گروه با یکدیگر متفاوت است.
2. تعیین سطح آلفا (α): سطح آلفا، که معمولاً 0.05 در نظر گرفته می‌شود، احتمال رد فرضیه صفر در صورتی که درست باشد را نشان می‌دهد.
3. محاسبه آماره آزمون F: آماره F، نسبت واریانس بین گروه‌ها به واریانس درون گروه‌ها است. فرمول محاسبه آن به شرح زیر است: F=MSwithin​MSbetween​​ که در آن:
   • MSbetween​ (Mean Square Between): میانگین مربعات بین گروه‌ها
   • MSwithin​ (Mean Square Within): میانگین مربعات درون گروه‌ها
4. تعیین درجه آزادی:
   • درجه آزادی بین گروه‌ها: dfbetween​=k−1 (k = تعداد گروه‌ها)
   • درجه آزادی درون گروه‌ها: dfwithin​=N−k (N = کل تعداد مشاهدات)
5. یافتن مقدار بحرانی F یا مقدار p-value:
   • با استفاده از جدول توزیع F با درجه آزادی‌های محاسبه شده و سطح آلفا، مقدار بحرانی F را پیدا می‌کنیم.
   • یا با استفاده از نرم‌افزارهای آماری، مقدار p-value مربوط به آماره F محاسبه شده را به دست می‌آوریم.
6. تصمیم‌گیری:
   • روش مقدار بحرانی: اگر آماره F محاسبه شده بزرگتر از مقدار بحرانی F باشد، فرضیه صفر رد می‌شود.
   • روش p-value: اگر مقدار p-value کمتر از سطح آلفا (α) باشد، فرضیه صفر رد می‌شود.
7. تفسیر نتایج: اگر فرضیه صفر رد شود، به این معنی است که حداقل بین میانگین‌های دو گروه تفاوت معناداری وجود دارد. برای تعیین اینکه کدام گروه‌ها با یکدیگر تفاوت دارند، معمولاً از آزمون‌های تعقیبی (Post-hoc tests) مانند آزمون توکی، بونفرونی یا شفه استفاده می‌شود.

کاربردهای گسترده آزمون آنوا

آزمون آنوا در زمینه‌های مختلف علمی و کاربردی مورد استفاده قرار می‌گیرد، از جمله:

• علوم تربیتی: مقایسه اثربخشی روش‌های مختلف آموزشی.
• کشاورزی: بررسی تاثیر انواع کودها بر عملکرد محصولات.
• روانشناسی: مقایسه میانگین نمرات اضطراب در گروه‌های مختلف درمانی.
• بازاریابی: ارزیابی تاثیر کمپین‌های تبلیغاتی مختلف بر فروش.
• پزشکی: مقایسه اثربخشی داروهای مختلف بر یک بیماری خاص.
• مهندسی: بررسی تاثیر پارامترهای مختلف تولید بر کیفیت محصول.

نرم‌افزارهای مورد استفاده برای آزمون آنوا

امروزه، نرم‌افزارهای آماری متعددی برای انجام آزمون آنوا و تحلیل‌های تکمیلی در دسترس هستند، از جمله:

• SPSS
• R
• SAS
• Minitab
• Excel (با استفاده از ابزار Analysis ToolPak)

این نرم‌افزارها فرآیند محاسبات پیچیده را تسهیل کرده و امکان تفسیر دقیق‌تر نتایج را فراهم می‌کنند.

مراحل انجام آزمون آنوا یک طرفه در SPSS

آزمون آنوا یک طرفه برای مقایسه میانگین‌های یک متغیر وابسته (کمی) بین سه گروه یا بیشتر از یک متغیر مستقل (کیفی) استفاده می‌شود. در SPSS برای انجام این آزمون مراحل زیر را دنبال کنید:

1. باز کردن دیالوگ باکس ANOVA:
   • از منوی اصلی SPSS، روی Analyze کلیک کنید.
   • از زیرمنوی باز شده، گزینه Compare Means را انتخاب کنید.
   • در نهایت، روی One-Way ANOVA… کلیک کنید تا پنجره مربوط به این آزمون باز شود.
2. تعیین متغیرها:
   • در پنجره One-Way ANOVA، لیستی از تمام متغیرهای موجود در دیتاست شما در سمت چپ نمایش داده می‌شود.
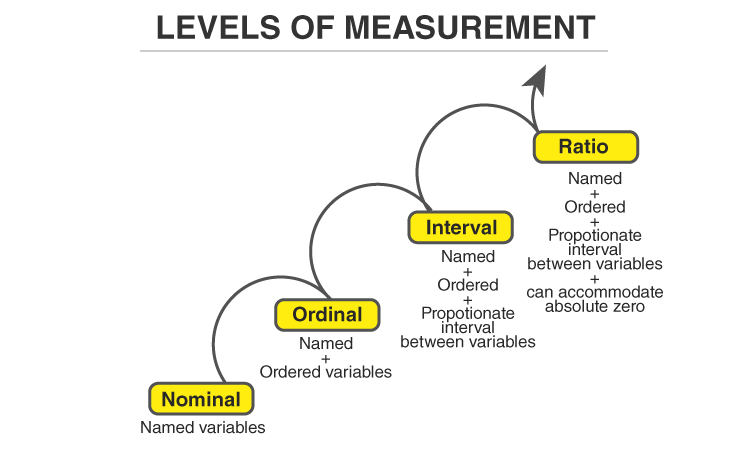
   • متغیر وابسته (Dependent Variable): متغیری که می‌خواهید میانگین آن را بین گروه‌ها مقایسه کنید را انتخاب کرده و با استفاده از دکمه فلش وسط، آن را به کادر Dependent List منتقل کنید. این متغیر باید در سطح سنجش فاصله‌ای یا نسبی باشد (متغیر کمی).
   • متغیر مستقل (Factor): متغیری که گروه‌ها را تعریف می‌کند (متغیر کیفی) را انتخاب کرده و با استفاده از دکمه فلش وسط، آن را به کادر Factor منتقل کنید. این متغیر باید در سطح سنجش اسمی یا رتبه‌ای باشد و حداقل سه سطح یا گروه داشته باشد.
3. تعیین آزمون‌های تعقیبی (Post Hoc Tests) – اختیاری اما توصیه شده:
   • اگر نتیجه آزمون آنوا نشان دهد که بین میانگین گروه‌ها تفاوت معناداری وجود دارد (یعنی فرضیه صفر رد شود)، شما نیاز دارید تا مشخص کنید کدام گروه‌ها به طور خاص با یکدیگر تفاوت دارند. برای این منظور از آزمون‌های تعقیبی استفاده می‌شود.
   • روی دکمه Post Hoc… کلیک کنید تا پنجره Post Hoc Multiple Comparisons باز شود.
   • در این پنجره، انواع مختلفی از آزمون‌های تعقیبی وجود دارد. انتخاب آزمون مناسب بستگی به فرضیات شما و ویژگی‌های داده‌هایتان دارد. برخی از آزمون‌های رایج عبارتند از:
     • Tukey’s HSD: برای مقایسه‌های زوجی زمانی که تعداد نمونه در گروه‌ها تقریباً برابر است و فرض برابری واریانس‌ها برقرار باشد.
     • Bonferroni: یک روش محافظه‌کارانه‌تر برای کنترل خطای نوع اول در مقایسه‌های چندگانه.
     • Scheffé: یک آزمون محافظه‌کارانه که برای همه انواع مقایسه‌های میانگین‌ها مناسب است.
     • LSD (Least Significant Difference): کمترین محافظه‌کاری را دارد و احتمال خطای نوع اول را افزایش می‌دهد.
     • اگر فرض برابری واریانس‌ها برقرار نباشد (که در مرحله 4 بررسی می‌شود)، می‌توانید از آزمون‌هایی مانند Games-Howell استفاده کنید.
   • آزمون‌های مورد نظر خود را انتخاب کرده و روی دکمه Continue کلیک کنید.
4. تعیین گزینه‌ها (Options):
   • روی دکمه Options… کلیک کنید تا پنجره One-Way ANOVA: Options باز شود.
   • در این پنجره می‌توانید تنظیمات مختلفی را انتخاب کنید:
     • Descriptive: برای نمایش آمار توصیفی مانند میانگین، انحراف معیار، تعداد نمونه و غیره برای هر گروه. توصیه می‌شود این گزینه را فعال کنید.
     • Homogeneity of variance test: برای انجام آزمون لون (Levene’s Test) به منظور بررسی فرض برابری واریانس‌ها بین گروه‌ها. توصیه می‌شود این گزینه را فعال کنید. اگر نتیجه این آزمون معنادار باشد (p < 0.05)، فرض برابری واریانس‌ها رد می‌شود و باید در تفسیر نتایج و انتخاب آزمون‌های تعقیبی دقت کنید.
     • Means plot: برای نمایش نمودار میانگین‌ها به همراه خطای استاندارد برای هر گروه. این نمودار می‌تواند به تجسم تفاوت‌های بین گروه‌ها کمک کند.
     • Missing Values: نحوه برخورد با داده‌های گمشده را تعیین کنید (معمولاً Exclude cases analysis by analysis انتخاب مناسبی است).
   • پس از انتخاب گزینه‌های مورد نظر، روی دکمه Continue کلیک کنید.
5. اجرای آزمون:
   • پس از تعیین متغیرها، آزمون‌های تعقیبی (در صورت نیاز) و گزینه‌ها، روی دکمه OK در پنجره One-Way ANOVA کلیک کنید تا آزمون اجرا شود.
6. تفسیر نتایج:
   • جدول Descriptives: این جدول آمار توصیفی متغیر وابسته را برای هر گروه شامل میانگین، انحراف معیار، تعداد نمونه و غیره ارائه می‌دهد.
   • جدول Test of Homogeneity of Variances: نتیجه آزمون لون را نشان می‌دهد. اگر مقدار Sig. (p-value) در این جدول بزرگتر از سطح آلفا (معمولاً 0.05) باشد، فرض برابری واریانس‌ها پذیرفته می‌شود. در غیر این صورت، این فرض رد می‌شود.
   • جدول ANOVA: مهم‌ترین جدول خروجی است. ستون F آماره F آزمون آنوا را نشان می‌دهد، ستون df درجات آزادی بین گروه‌ها و درون گروه‌ها را نشان می‌دهد و ستون Sig. مقدار p-value آزمون را ارائه می‌کند.
     • اگر مقدار Sig. کمتر از سطح آلفا باشد، فرضیه صفر (برابری میانگین تمام گروه‌ها) رد می‌شود و نتیجه می‌گیریم که حداقل بین میانگین‌های دو گروه تفاوت معناداری وجود دارد.
   • جدول Multiple Comparisons (در صورت انتخاب آزمون‌های تعقیبی): این جدول نتایج مقایسه‌های زوجی بین گروه‌ها را نشان می‌دهد. برای هر زوج گروه، تفاوت میانگین، خطای استاندارد، سطح معناداری (Sig.) و فاصله اطمینان (Confidence Interval) ارائه می‌شود. با بررسی مقدار Sig. می‌توانید مشخص کنید کدام زوج گروه‌ها تفاوت معناداری دارند.

با دنبال کردن این مراحل، می‌توانید آزمون آنوا یک طرفه را در SPSS انجام داده و نتایج آن را برای تحلیل داده‌های پژوهش خود تفسیر کنید. به یاد داشته باشید که گزارش نتایج باید شامل آماره F، درجات آزادی و مقدار p-value از جدول ANOVA و همچنین نتایج آزمون‌های تعقیبی (در صورت معنادار بودن آزمون آنوا) باشد.

جمع‌بندی

آزمون آنوا یک ابزار قدرتمند در جعبه ابزار آماری هر محقق و تحلیلگری است. با درک مفاهیم اساسی، فرضیات و مراحل اجرای این آزمون، می‌توانید به طور موثر میانگین‌های چند گروه را مقایسه کرده و به بینش‌های ارزشمندی از داده‌های خود دست یابید. به یاد داشته باشید که بررسی فرضیات آزمون و استفاده از آزمون‌های تعقیبی در صورت رد فرضیه صفر، برای دستیابی به نتایج دقیق و قابل اعتماد ضروری است.

امیدواریم این راهنمای جامع، درک شما از آزمون آنوا را بهبود بخشیده باشد. اگر سوالی دارید، در بخش نظرات با ما در میان بگذارید.

ابوالفضل پایروند